DIBUJO TÉCNICO

COMO ESTÁN......

Aquí aprenderás de una forma fácil y sencilla a realizar trabajos de dibujo técnico paso a paso y de forma gratuita.

De la misma forma debemos de interactuar juntos como comunidad educativa para lograr muchos avances.

Gracias por su participación. Saludos cordiales.

Curvas cónicas : elipse

Definición :
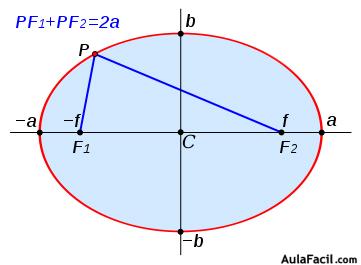
La elipse es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos, es constante e igual al radio mayor de la elipse.

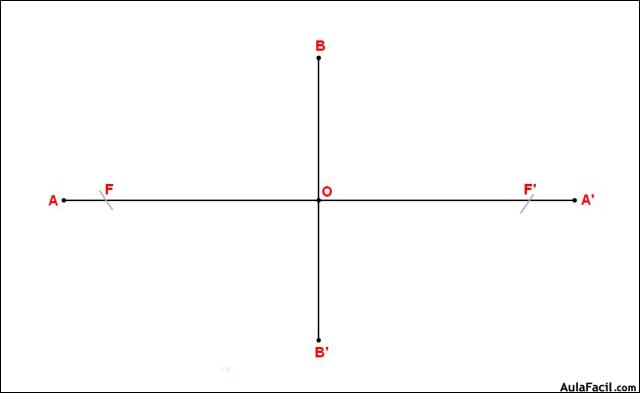
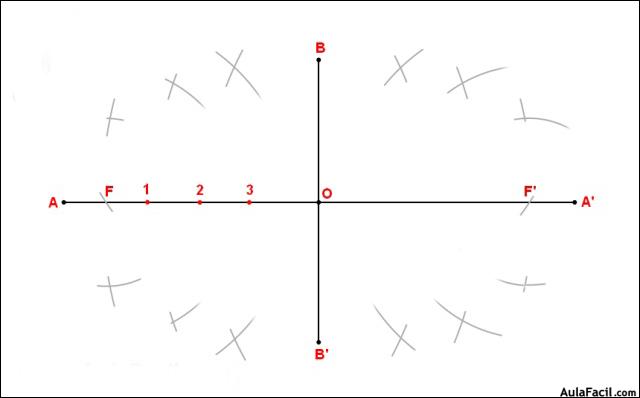
Construcción de la elipse a partir de sus ejes :

1. Primero buscamos los focos. Para ello, con la medida AO trazamos un arco con centro en B que determina los focos en AA'.

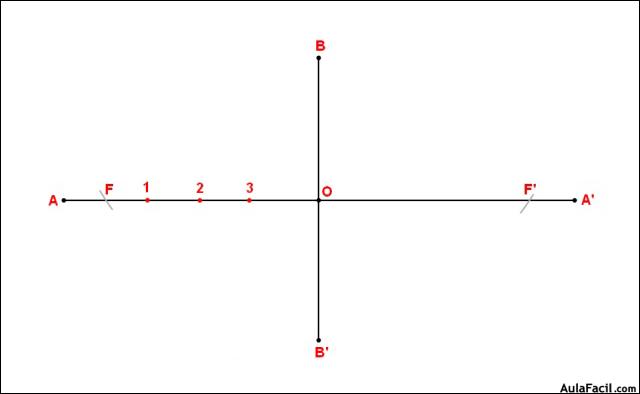
2. Marcamos 3 puntos cualquiera entre F y O

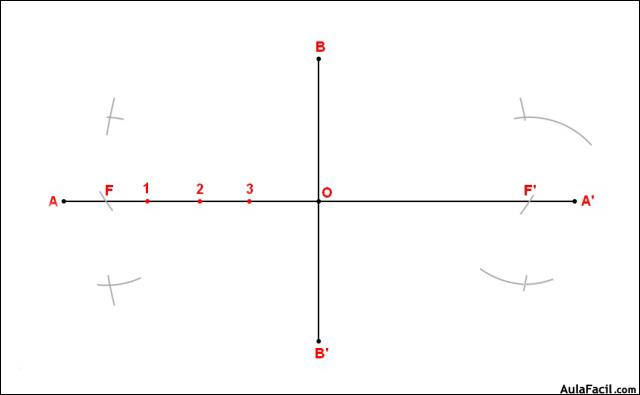
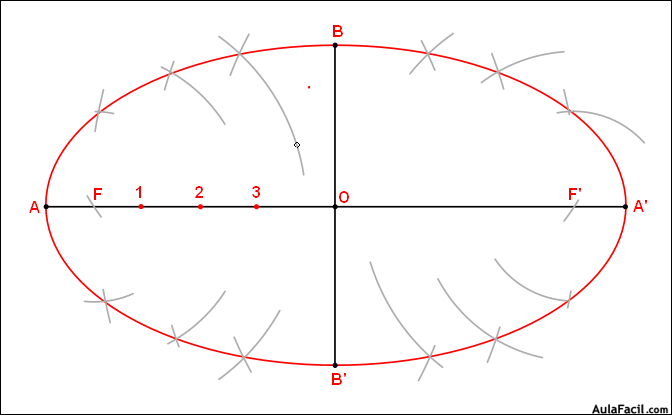
3. Con radios A1 y 1A' y centros en F y F' trazamos arcos. Donde se corten quedarán determinados los cuatro primeros puntos de la elipse.

4. Realizamos el mismo proceso con los puntos 2 y 3 y obtendremos los puntos de referencia de la elipse.

5. Uniendo los puntos resultantes con los extremos de los ejes quedará dibujada nuestra elipse.

Curvas cónicas : parábola

Definición :
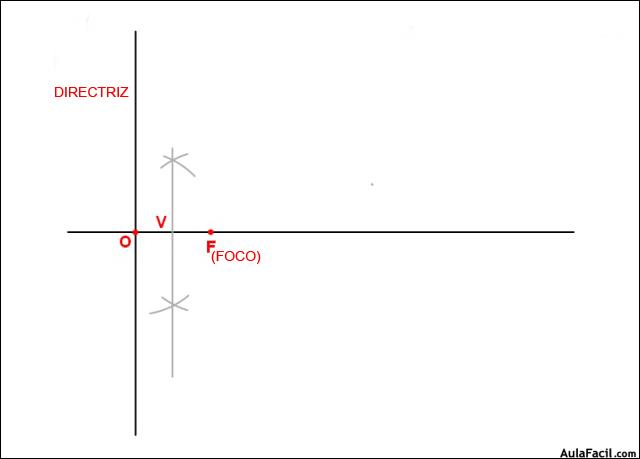
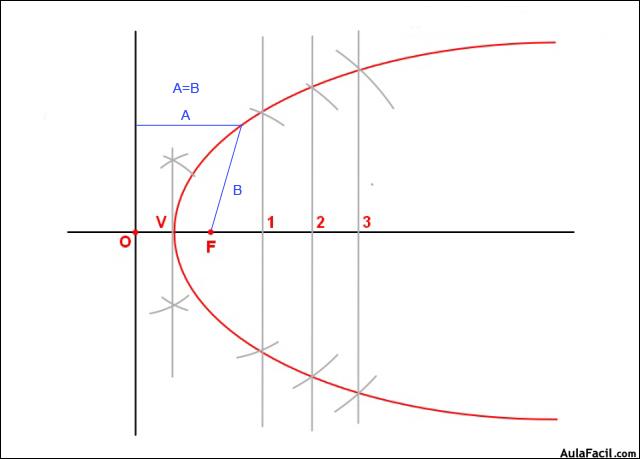
La Parábola es el lugar geométrico de los puntos del plano cuyas distancias a un punto fijo, llamado foco, y a una recta, llamada directriz, son equidistantes.

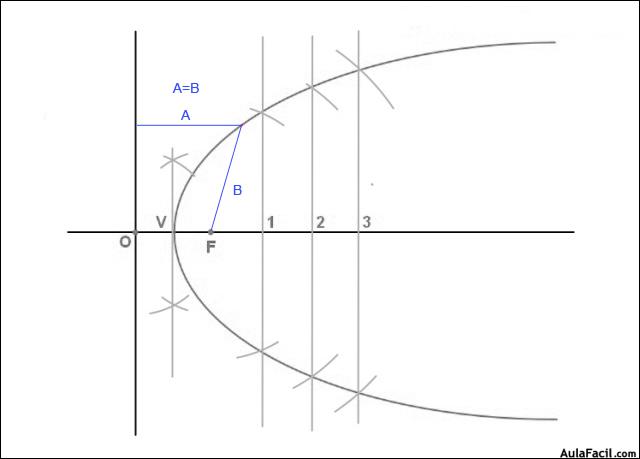
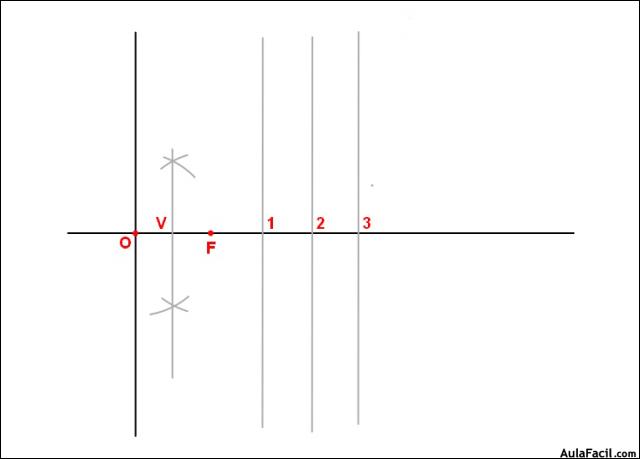
Construcción de la parábola por puntos conociendo sus ejes :

1. Hallamos el punto medio de OF que es el vértice V de nuestra parábola.

2. Marcamos una serie de puntos sobre el eje de nuestra parábola y trazamos por esos puntos rectas paralelas a la directriz.

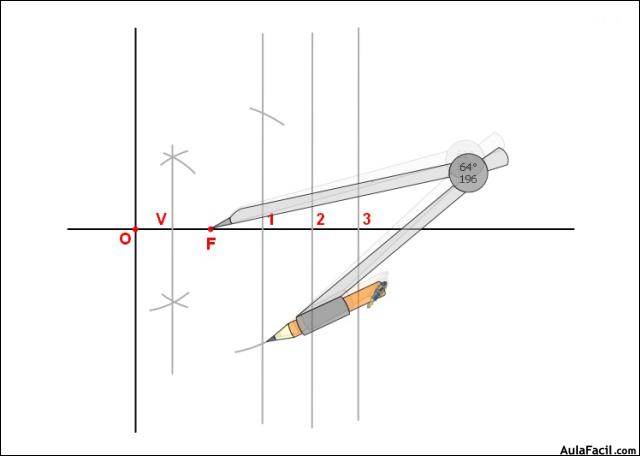
3. Con radio O1 y centro en F trazamos un arco que corta a la paralela por 1 en dos puntos que pertenecen a la parábola.

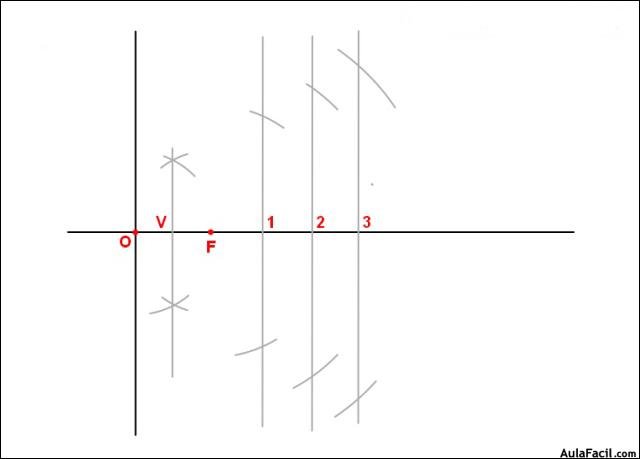
4. Repetimos la operación con los puntos 2 y 3 con radio O2 y O3 respectivamente y centro F.

5. Unimos los puntos encontrados y el vértice y queda definida la parábola.